Bewegung [1]
[765] Bewegung ist stetige Ortsveränderung. Sie ist ihrem Wesen nach etwas Relatives, insofern die den Ort bestimmenden Elemente, z.B. ein Koordinatensystem, selbst wieder bewegt gedacht werden können. Wird das Koordinatensystem, auf das die bewegten Gebilde bezogen werden, als ruhend vorausgesetzt, so nennt man die Bewegung absolut, andernfalls relativ in bezug auf das betreffende Koordinatensystem.
Die Bewegung eines Punktes wird durch die Gesamtheit seiner Lagen (die Bahn) und die Geschwindigkeit, mit der er von einer Lage zur benachbarten übergeht, gekennzeichnet. Bei gleichförmiger Bewegung ist die Geschwindigkeit υ konstant und der auf der Bahn zurückgelegte Weg s proportional der Zeit s = υt. Faßt man die Geschwindigkeit als gerichtete Größe [υ] auf, so ist ihre Richtung jene der Bahntangente und ihre Größe υ = ds : dt, wenn ds das in der Zeit dt zurückgelegte Kurvenelement bedeutet. In diesem Sinn genommen ist die Bewegung mit gleichbleibender Geschwindigkeit stets geradlinig. Unter Beschleunigung [φ] als gerichtete Größe aufgefaßt, versteht man das Verhältnis der in dem Zeitelement dt erfolgten Geschwindigkeitsänderung (Elementarbeschleunigung) [dυ] zu dt : [φ] = [dυ]/dt. Die in diesem Sinne gleichförmig beschleunigte Bewegung ist die parabolische Wurfbewegung. Die Bewegung heißt frei, wenn sie bloß durch äußere beschleunigende Kräfte bewirkt wird. Ist die Bahn des Punktes gegeben oder durch Bedingungen, z.B. das Verbleiben auf einer Fläche eingeschränkt, so heißt die Bewegung gezwungen. Die gezwungene Bewegung wird dadurch auf eine freie zurückgeführt, daß man den Einfluß der vorgeschriebenen Bahn oder sonstiger Bedingungen durch entsprechende Kräfte ersetzt, z.B. beim Kreispendel durch die Fadenspannung.
Die Bewegung eines Systems von Punkten kann auf die Bewegung der Einzelpunkte zurückgeführt werden. Am einfachsten ist die Bewegung eines starren Systems. Zwei aufeinander folgende Lagen können durch eine unendlich kleine Schraubenbewegung ineinander übergeführt werden. Diese Schraubenbewegung wird durch ihre Achse (Momentanachse), die Elementardrehung dϑ um dieselbe und die Elementarverschiebung dτ längs derselben gekennzeichnet. Durch Division mit dem Zeitelement dt, innerhalb deren die Bewegung ausgeführt wird, erhält man die Winkelgeschwindigkeit w = dϑ/dt und die Verschiebungsgeschwindigkeit dτ/dt = υ0. Bei der elementaren Schraubenbewegung beschreibt jeder Punkt das Element einer Schraubenlinie, das in der Entfernung r von der Achse unter einem Winkel ctg α = υ0/rw gegen dieselbe geneigt ist. Der Quotient υ0/w = p heißt der Parameter der Schraubenbewegung. Jede Schraubenbewegung kann auf unzählige Weisen durch die Verbindung einer Drehbewegung um eine zur Momentanachse parallele Achse und eine beliebig gerichtete Parallelverschiebung ersetzt werden (s. Aequivalenz der Bewegungen). Sind die Momentanachsen dauernd parallel und ist υo = 0, so entsteht die ebene Bewegung, bei der alle Punkte ebene Kurven senkrecht zur Stellung der Momentanachsen beschreiben. Ist ein Punkt des starren Systems fest, so gehen alle Momentanachsen durch diesen Punkt, und die übrigen Systempunkte beschreiben sphärische Kurven auf konzentrischen Kugeln: sphärische Bewegung.
Im allgemeinen Fall bilden die sämtlichen Momentanachsen eines starren Systems eine geradlinige (windschiefe oder abwickelbare) Fläche (Γ), die mit dem Koordinatensystem in fester Verbindung fleht. Man kann aber auch jede Momentanachse als Bestandteil des bewegten Systems auffallen, und die Gesamtheit dieser Bestandteile bildet eine zweite, mit dem bewegten System verbundene geradlinige Fläche (C). Bei der Bewegung des Systems dreht sich die Fläche (C) um die mit (Γ) gemeinsame Gerade (Momentanachse) und verschiebt sich längs derselben. Diese Bewegung der Fläche (C) an der Fläche (Γ) heißt Schrotung. Im Falle der ebenen Bewegung werden die Flächen (Γ) und (C) Zylinder mit Erzeugenden senkrecht zur Ebene der Bewegung, und die Schrotung geht in das Abrollen des Zylinders (C) an den Zylinder (Γ) über. Bei der sphärischen Bewegung werden die Flächen (Γ) und (C) Kegel mit gemeinsamer Spitze im festen Punkt, wobei der Kegel (C) auf den Kegel (Γ) abrollt.
Ebene Bewegung oder Bewegung eines ebenen unveränderlichen Punktsystems in der Ebene. Das bewegliche System sei Σ und A, B, C, ... irgendwelche Punkte desselben; Σ1 (A1, B1, C1, ....) eine erste, Σ2 (A2, B2, C2, ....) eine zweite Lage desselben in der Ebene ε der Bewegung. Diese[765] beiden Lagen sind kongruente Systeme und haben einen Doppelpunkt, in dem zwei homologe Punkte P1P2 zusammenfallen. Man findet dieselben, indem man zwei Verbindungssehnen A1A2 und B1B2 rechtwinklig halbiert; die Halbierungslinien schneiden lieh in ihm. Daher kann Σ aus der Lage Σ1 in die Lage Σ2 durch Rotation um den Punkt P, der in dem Doppelpunkte P1P2 ruht, übergeführt werden. Sind Σ1 und Σ2 unmittelbar aufeinander folgende Lagen von Σ, so gehen die Geraden A1A2 und B1B2 in die Tangenten der Bahnen von A und B und A1P1, B1P1 in deren Normalen über. Man ersieht hieraus, daß in jedem Momente der Bewegung von Σ in der Ebene ε ein Punkt desselben existiert, um den dasselbe eine unendlich kleine Rotation erleidet, um in die unmittelbar folgende Lage zu gelangen. Dieser Punkt ist das der betreffenden Lage entsprechende Momentanzentrum Γ, die unendlich kleine Rotationsamplitude dδ um dasselbe die Elementaramplitude und die unendlich kleine Bewegung selbst die Elementarbewegung des Systems Σ.
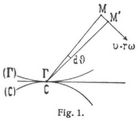
Das Momentanzentrum ist der Punkt des beweglichen Systems Σ, der augenblicklich ruht; dasselbe hat in ε eine bestimmte Lage C. Alle Punkte M des Systems beschreiben momentan Bahnelemente, die als Elemente M M' vom Kreisbogen anzusehen sind (Fig. 1), beschrieben mit den Abständen M Γ der Punkte vom Momentanzentrum als Radien. Die Geraden M Γ sind daher die Normalen und senkrecht zu ihnen laufen die Tangenten der Bahnen. In jedem Momente der Bewegung laufen die Normalen der Bahnen aller Systempunkte durch das Momentanzentrum. Die kontinuierliche Folge aller den verschiedenen Lagen von Σ entsprechenden Momentanzentren Γ bildet eine Kurve (Γ), die dem System angehört; die Lagen C desselben bilden eine andre, der Ebene ε der Bewegung angehörige Kurve (C). Beide Kurven berühren lieh im betreffenden Momentanzentrum Γ, C. Die Geschwindigkeit ν des Systempunktes M ist υ = M M'/dt = MC ∙ dδ/dt = r ∙ dδ/dt, wenn Γ, C das der Zeit t entsprechende Momentanzentrum und r der Abstand desselben von diesem ist. Die Geschwindigkeit aller Systempunkte im Abstande r = 1 ist ω = dδ/dt und heißt die Winkelgeschwindigkeit um das Momentanzentrum. Demnach ist die Geschwindigkeit υ = rω, also für alle Punkte auf einem mit dem Radius r um das Momentanzentrum beschriebenen Kreise von derselben Größe; sie ist Null im Momentanzentrum und wächst proportional dem Abstande r von ihm; auf einem durch C gezogenen Strahle hat sie auf entgegengesetzten Seiten entgegengesetzten Sinn.
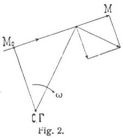
Die Geschwindigkeiten der Punkte M einer Geraden des Systems, die nicht durch das Momentanzentrum hindurchgeht, haben ein Minimum, das nicht Null ist. Der Fußpunkt Mo des vom Momentanzentrum auf die Gerade gefällten Perpendikels hat die kleinste Geschwindigkeit, ihre Richtung fällt in die Gerade selbst (Fig. 2). Dieser Punkt heißt der Gleitungspunkt der Geraden und ist der Berührungspunkt derselben mit der Kurve, welche die Gerade während der Bewegung des Systems umhüllt. Es gehen daher auch die Normalen aller von den verschiedenen Geraden des Systems umhüllten Kurven in ihren Berührungspunkten mit diesen durch das der Lage des Systems entsprechende Momentanzentrum hindurch. – Zerlegt man die Geschwindigkeiten der Punkte einer Systemgeraden jede in zwei Komponenten, eine von der Richtung der Geraden, die andre senkrecht zu ihr, so ergibt sich, daß die ersteren alle gleich, nämlich gleich der Geschwindigkeit des Gleitungspunktes sind. Die Bewegung der Geraden um das Momentanzentrum kann gespalten werden in eine Translation derselben von ihrer Richtung und in eine Rotation um den Gleitungspunkt. Die Geschwindigkeit der Translation ist die Geschwindigkeit des Gleitungspunktes und die Winkelgeschwindigkeit der Rotation ist die Winkelgeschwindigkeit <w um das Momentanzentrum. Wegen der Relativität des Bewegungsbegriffes ist mit jeder Bewegung des ebenen Systems Σ in der Ebene ε eine andre Bewegung verbunden. Die Ebene ε stellt nämlich selbst ein ebenes System dar, das in Σ ebenso gut seine Lage ändert, also sich in Σ bewegt, wie Σ in e. Beide Bewegungen heißen Umkehrungen voneinander und diese Duplizität der Bewegung der Dualismus derselben (s.d.). Für die Umkehrung der Bewegung verlaufenen die Kurven (Γ) und (C) ihre Rollen. Während bei der einen (Γ) über (C) hinrollt, ohne zu gleiten, rollt bei der andern (C) über (Γ) im umgekehrten Sinne. Die ebene Bewegung ist durch zwei Bedingungen bestimmt. Das bewegliche System Σ ist nämlich aus einer Lage in die nächstfolgende mit allen Punkten übergegangen, sobald dies mit zweien seiner Punkte erfolgt ist. Insbesondere ist daher die Bewegung bestimmt: a. durch zwei Kurven als die Bahnen zweier Systempunkte, b. durch zwei Kurven, die Umhüllungskurven von zwei Systemgeraden sind, c. durch zwei Kurven, die von zwei Systemkurven fortwährend berührt werden. Die Umkehrung hiervon liefert noch die Bestimmung: d. durch zwei Kurven, die durch zwei Punkte hindurchgehen. Von diesen Bestimmungsarten sind zahlreiche Spezialisierungen möglich, indem Kurven in Punkte oder Geraden degenerieren, zwei berührende Kurven in eine doppelt berührende Kurve ausarten u.s.w.
Die beiden Orte (Γ), (C) der Momentanzentra sind die einzigen Kurven, die während der Bewegung aufeinander rollen, ohne zu gleiten. Jede andre Systemkurve umhüllt eine Enveloppe,[766] so daß sie auf ihr rollt und gleitet, indem sich der Berührungspunkt auf der gemeinsamen Tangente verschiebt und die Kurve sich um ihn umdreht.
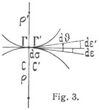
Das Momentanzentrum Γ, C wechselt im allgemeinen in jedem Momente der Bewegung. Ist dσ das Bogenelement ΓΓ' = CC', mit dem sich die beiden Kurven (Γ) und (C) zur Zeit t berühren (Fig. 3), so heißt u = dσ/dt die Wechselgeschwindigkeit des Momentanzentrums, entsprechend dieser Zeit. Sie ist nicht die Geschwindigkeit eines dem System angehörigen Punktes, sondern im gewissen Sinne eine Fortpflanzungsgeschwindigkeit der Bewegung. Das Verhältnis der Winkelgeschwindigkeit ω und der Wechselgeschwindigkeit u des Systems kann durch die Krümmungen der Kurven (Γ) und (C) dargestellt werden. Fallen nämlich die Krümmungskreise beider Kurven auf entgegengesetzte Seiten der gemeinsamen Tangente und sind dε, dε' die Kontingenzwinkel und ρ = dσ/dt, ρ' = dσ/dε' die Krümmungshalbmesser von (C) und (Γ), so ist dδ = dε + dε' die Amplitude der Elementarbewegung und
fallen aber die Krümmungskreise auf dieselbe Seite der gemeinsamen Tangente und ist ρ < ρ', so wird dδ = dε – dε' und w/u = 1/ρ – 1/ρ', im Falle ρ > ρ' aber dδ = dε – dε' und w/u = – (1/ρ – 1/ρ'). In den beiden letzten Fällen haben die Elementarbewegungen entgegengesetzten Sinn. Wird bei gleichartiger Lage der Krümmungskreise gegen die gemeinschaftliche Tangente ρ = ρ', so erfolgt ein momentaner Stillstand der Bewegung, indem w/u = 0 wird. Man kann leicht alle diese Einzelfälle in eine Formel zusammenfassen, indem man den Krümmungshalbmessern ρ, ρ' besondere Vorzeichen gibt, übereinstimmend mit der Lage der Krümmungskreise. Die Hauptprobleme der ebenen Bewegung sind: 1. die Auffindung des Momentanzentrums Γ, C entsprechend einer gegebenen Lage des Systems; 2. die Bestimmung der Orte (Γ), (C) aller Momentanzentra im System Σ, sowie in der Ebene ε der Bewegung; 3. die Bestimmung der Bahn eines beliebigen Systempunktes; 4. die der Umhüllungskurve einer Systemgeraden. Die Behandlung dieser Aufgaben hängt von den beiden Bedingungen ab, welche die Bewegung definieren und kann synthetisch und analytisch gefordert werden. – Die Bahnen der Systempunkte bilden eine Kurvenschar, deren Individuen kontinuierlich ineinander übergehen. Für die Technik ist der Fall besonders wichtig, daß in dieser Schar geradlinige Bahnen vorkommen (Geradführungen). Weiteres s. Beschleunigung und Beschleunigungszentrum.
Umkehrung der Bewegung.
Zu jeder Bewegung eines starren Systems gehört eine Umkehrung, die aus der Relativität des Begriffes der Bewegung folgt. Man kann das starre System als ruhend auffassen, dann bewegt sich das Koordinatensystem und dessen Bewegung heißt die Umkehrung der ursprünglichen Bewegung. Dabei vertauschen die Flächen (C) und (Γ) ihre Rollen; (C) bleibt ruhend und (Γ) schrotet längs (C). Den Fall ebener Bewegung s. oben.
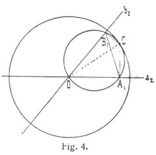
Als Beispiel für die Umkehrung einer Bewegung möge die verallgemeinerte elliptische Bewegung von Cardano dienen (Fig. 4). Eine Ebene ε1 bewegt sich in der Ebene ε2 so, daß zwei ihrer Punkte A1B1 fortwährend auf zwei Geraden a2b2 von ε2 bleiben. Die Momentanachse geht dabei durch den Punkt C, in denen sich die Lote in A1 auf a2 und B1 auf b2 schneiden, und steht senkrecht auf den Ebenen ε1 ε2. In der Ebene ε2 bilden die Punkte C einen Kreis mit dem Mittelpunkt O im Schnittpunkt von a2b2, in der Ebene ε1 einen Kreis von halbem Radius, der über der Sehne A1B1 den Winkel der Geraden a2b2 als Peripheriewinkel faßt. Die Bewegung von ε1 kann durch das Rollen des letzteren Kreises auf der Innenseite des ersteren erzeugt werden, wobei alle Punkte von ε1 in ε2 konzentrische Ellipsen um den Punkt O beschreiben (Fig. 1). Die Umkehrung der Bewegung ist jene, bei der die Ebene ε2 sich so bewegt, daß die in ihr liegenden Geraden von a2b2 stets durch die festen Punkte A1B1 der Ebene ε1 gehen. Bei dieser Bewegung rollt der erstgenannte große Kreis mit seiner Innenseite auf dem kleinen Kreise ab, und jeder Punkt der Ebene ε2 beschreibt in ε1 eine Paskalsche Schnecke.
Ueber die Bewegung nichtstarrer Systeme lassen sich nur bei kontinuierlichen Systemen (wie Flüssigkeiten, elastischen Körpern) allgemeine Aussagen machen. Die Veränderung eines unendlichkleinen Bereiches eines solchen Systems nach Ablauf einer endlichen Zeit läßt sich als (nichtvertauschbare) Aufeinanderfolge dreier Einzelbewegungen auffassen: erstens einer Verschiebungsbewegung, die einen Punkt des als starrgedachten Bereichs in seine neue Lage bringt, zweitens einer Drehbewegung um eine bestimmte Achse durch diesen Punkt um einen endlichen Winkel, drittens einer homogenen Deformation (affinen Veränderung) des Bereichs in drei zueinander senkrechten Richtungen (Achsen der Deformation) in endlichem Betrage, wobei der genannte Punkt unverändert bleibt. Nimmt man die abgelaufene Zeit als unendlichklein an und dividiert man mit ihr die nun ebenfalls unendlichklein gewordenen Veränderungen, so erhält man eine Verschiebungsgeschwindigkeit, eine Winkelgeschwindigkeit und drei Deformationsgeschwindigkeiten, die im Verein mit der Verschiebungsrichtung, der[767] Drehachse und den drei Deformationsrichtungen die Momentanbewegung des Bereiches bestimmen. Die Bewegung heißt wirbelfrei, wenn in allen Punkten des Systems die Winkelgeschwindigkeit verschwindet. Sie heißt quellenfrei, wenn die homogene Deformation in allen Punkten das Volumen nicht ändert. Die Bewegung eines starren Systems ist stets quellenfrei, dagegen nur im Falle reiner Parallelverschiebung wirbelfrei.
Relative Bewegung.
Bewegt sich ein Punkt oder ein Punktsystem in einem Koordinatensystem, das selbst eine Bewegung gegenüber einem andern ruhend gedachten Koordinatensystem ausführt, so entsteht eine zusammengesetzte Bewegung jenes Punktes oder Punktsystemes. Sie kann auch als absolute Bewegung im ruhenden Koordinatensystem aufgefaßt werden. Die Bewegung des Punktes oder Punktsystemes im bewegten Koordinatensystem heißt dann relative Bewegung. Hält man den Punkt oder das Punktsystem im bewegten Koordinatensystem fest, so hat er, bezw. das Punktsystem, infolge der Bewegung dieses Koordinatensystems noch die so genannte Führungsbewegung. Den drei Bewegungen entsprechend unterscheidet man auch dreierlei Geschwindigkeiten und Beschleunigungen, absolute, relative und Führungsgeschwindigkeiten, bezw. Beschleunigungen. Die absolute Geschwindigkeit ist die geometrische Summe (= Resultante) der relativen und der Führungsgeschwindigkeit. Die absolute Beschleunigung [φ] setzt sich dagegen als Resultante dreier Beschleunigungen (s. Beschleunigung) zusammen: relative Beschleunigung [φr], Führungsbeschleunigung [φs] und zusammengesetzte Zentrifugalbeschleunigung oder Coriolische Beschleunigung [φω], [φ] = [φr] + [φs] + [φω]. Letztere steht senkrecht auf einer durch den bewegten Punkt und die Momentanachse des bewegten Koordinatensystems gelegten Ebene und ihre Größe ist gleich dem Produkt aus der Winkelgeschwindigkeit um die Momentanachse und der Projektion der relativen Geschwindigkeit auf eine zur Momentanachse senkrechte Ebene. Sind p, q, r die Komponenten der Winkelgeschwindigkeit nach den Achsen des bewegten Systems und x, y, z die Koordinaten des bewegten Punktes im gleichen System, so sind die drei Komponenten φωx, φωy, φωz, der zusammengesetzten Zentrifugalbeschleunigung nach den Achsen des bewegten Koordinatensystems durch folgende Formeln gegeben:
Multipliziert man die Resultantengleichung [φ] = [φr] + [φs] + [φω] beiderseits mit der Masse des bewegten Punktes und stellt sie um, so erhält man: m [φr] = m [φ] – m [φs] – m [φω]. – Vgl. a. Beschleunigung.
Die Produkte aus Masse mal Beschleunigung kann man als Kräfte, die die Bewegung verursachen, deuten. Nur m [φ] ist eine wirkliche, auf den Punkt wirkende Kraft, die andern sind scheinbare. Der Sinn obiger Gleichung läßt sich dann, wie folgt, aussprechen: Die relative Bewegung eines Punktes erfolgt so, wie wenn auf ihn eine Kraft (= m [φr]) wirkte, die sich aus der tatsächlich wirkenden Kraft (= [φ]), der entgengesetzten Zentrifugalkraft (= – m[φs]) und der entgegengesetzten Coriolischen Kraft (= – [φω]) zusammensetzte. Dabei ist das Koordinatensystem, in dem die relative Bewegung des Punktes verfolgt wird, als ruhend vorausgesetzt.
Von den beiden (scheinbaren) Zusatzkräften hängt die erstere, nämlich die Zentrifugalkraft, bei unveränderter Bewegung des Koordinatensystems nur vom Ort des Punktes ab, die Coriolische Kraft dagegen von der Geschwindigkeit des bewegten Punktes. Erstere ist von den übrigen konstant wirkenden Kräften meist nicht zu trennen, dagegen bildet das Antreten von Kräften, die von der Geschwindigkeit abhängen, ein Kennzeichen der Bewegung des Koordinatensystems, auf das die betrachtete Bewegung bezogen ist. Die Lehre von der relativen Bewegung greift in alle Bewegungsvorgänge auf der rotierenden Erde ein. Die Zentrifugalkraft bewirkt hierbei nur eine kleine Veränderung der Lotrichtung, die in der Regel als Z-Achse des Koordinatensystems angenommen wird. Die Coriolische Kraft kommt dagegen in der Bewegung selbst zum Ausdruck und bewirkt beispielsweise, daß die Bahn eines Geschosses in der Horizontalprojektion nicht geradlinig ist, sondern vom Schützen aus gesehen nach rechts gekrümmt. Ein freifallender Stein fällt nicht genau in der Lotrichtung abwärts, sondern wird nach Osten abgelenkt. Unter dem Einfluß der Coriolischen Kraft wird die Schwingungsebene eines Fadenpendels dem Uhrzeigersinn entgegengesetzt gedreht. Alle diese Abweichungen bilden Beweise für die Drehung der Erde.
(Schell) Finsterwalder.
Brockhaus-1911: Los-von-Rom-Bewegung · Ethische Bewegung · Bewegung
DamenConvLex-1834: Bewegung der Erde · Bewegung (Musik) · Bewegung
Eisler-1904: Willkürliche Bewegung · Bewegung · Bewegung · Quantität der Bewegung
Kirchner-Michaelis-1907: Bewegung
Lueger-1904: Geradlinige Bewegung · Geometrie der Bewegung · Freiheitsgrade der Bewegung · Prinzip der Bewegung des Massenmittelpunktes (Schwerpunktes) · Parabolische Bewegung · Krummlinige Bewegung · Energie der Bewegung · Bewegung [3] · Bewegung [2] · Aperiodische Bewegung · Dualismus der Bewegung · Differentialgleichungen der Bewegung · Bewegung [4]
Meyers-1905: Pedētische Bewegung · Pankeltische Bewegung · Stationäre Bewegung · Revolutive Bewegung · Ethische Bewegung · Bewegung · Oxforder Bewegung · Los von Rom-Bewegung
Pierer-1857: Wurmförmige Bewegung des Darmkanals · Erste Bewegung · Bewegung
Buchempfehlung
Schnitzler, Arthur
Komtesse Mizzi oder Der Familientag. Komödie in einem Akt
Ein alternder Fürst besucht einen befreundeten Grafen und stellt ihm seinen bis dahin verheimlichten 17-jährigen Sohn vor. Die Mutter ist Komtesse Mizzi, die Tochter des Grafen. Ironisch distanziert beschreibt Schnitzlers Komödie die Geheimnisse, die in dieser Oberschichtengesellschaft jeder vor jedem hat.
34 Seiten, 3.80 Euro
Im Buch blättern
Ansehen bei Amazon
Buchempfehlung
Romantische Geschichten. Elf Erzählungen
Romantik! Das ist auch – aber eben nicht nur – eine Epoche. Wenn wir heute etwas romantisch finden oder nennen, schwingt darin die Sehnsucht und die Leidenschaft der jungen Autoren, die seit dem Ausklang des 18. Jahrhundert ihre Gefühlswelt gegen die von der Aufklärung geforderte Vernunft verteidigt haben. So sind vor 200 Jahren wundervolle Erzählungen entstanden. Sie handeln von der Suche nach einer verlorengegangenen Welt des Wunderbaren, sind melancholisch oder mythisch oder märchenhaft, jedenfalls aber romantisch - damals wie heute. Michael Holzinger hat für diese preiswerte Leseausgabe elf der schönsten romantischen Erzählungen ausgewählt.
- Ludwig Tieck Die beiden merkwürdigsten Tage aus Siegmunds Leben
- Karoline von Günderrode Geschichte eines Braminen
- Novalis Heinrich von Ofterdingen
- Friedrich Schlegel Lucinde
- Jean Paul Die wunderbare Gesellschaft in der Neujahrsnacht
- Adelbert von Chamisso Peter Schlemihls wundersame Geschichte
- E. T. A. Hoffmann Der Sandmann
- Clemens Brentano Die drei Nüsse
- Ludwig Achim von Arnim Der tolle Invalide auf dem Fort Ratonneau
- Wilhelm Hauff Jud Süss
- Joseph von Eichendorff Das Schloß Dürande
442 Seiten, 16.80 Euro
Ansehen bei Amazon
- ZenoServer 4.030.014
- Nutzungsbedingungen
- Datenschutzerklärung
- Impressum